真随机与伪随机
真随机数是指我们完全无法预测的随机,比如利用电子自旋进行的设计。伪随机数的原因是输出的结果是有规律的,可以根据电路设计和生成算法进行预测。一般基于CMOS器件的电路设计中一般用到的是伪随机数发生器。伪随机数也有很多方法,比如:
- 线性的乘法$out = a \times x + b$,其中$a$和$b$是两个定值,$x$ 作为种子(seed)。
- 每个时钟周期都自加1。
考虑到硬件资源,更为简单的设计方案:LFSR。
LFSR (Linear Feedback Shift Registers)
LFSR每一个时钟周期都可以输出一个数字序列,其方案如图所示:
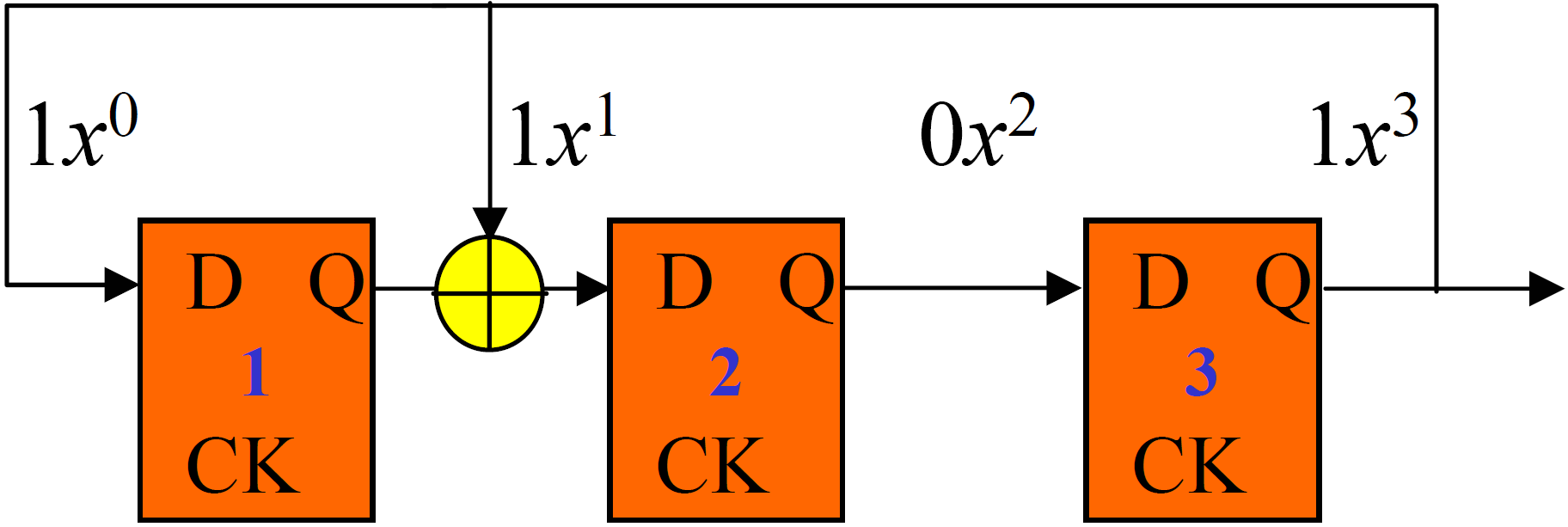
其多项式可以写成$P(x) = x^3 + x + 1$:
- $x^n$ 是多项式的阶数(degree);
- 系数$0$或$1$代表有没有反馈(有反馈的位置是异或运算)。
这样一个结构中的所有寄存器的数值组合可以呈现周期变化。不同的多项式$P(x)$产生的序列循环周期和顺序不同。循环的周期最大为$2^k - 1$,其中k是寄存器的个数。
本源多项式 (Primitive Polynomial)
使LFSR的循环周期最大(即$2^k - 1$)的多项式$P(x)$叫本源多项式。最少的反馈(异或门)构成的本源多项式如下:

Note
- 不能状态全为0,因为这会使状态无法自主切换(一直卡在为全0的状态)
参考:http://www.eng.auburn.edu/~strouce/class/elec6250/LFSRs.pdf